Prime numbers are positive integers with only 2 factors: 1 and themselves. In other words, these are numbers that can only be perfectly divided by 1 and themselves. One is not a prime number because it only has one factor. A factor is a number or algebraic expression that divides another number or expression evenly; with no remainder.

For example, 2 and 4 are factors of 16 because 16÷ 2 = 8 exactly and 16 ÷ 4 = 4 exactly. The other factors of 16 are 1, 8, and 16.

Take 13 as an example; we would need to divide 13 by every number from 2 to 13 to check if we get a perfect division. We can do this using the modulo. The modulus operator (%) in python gives the remainder after division.

For example:

13 % 2 -> 1 # 13/2 = 6 remainder 1

13 % 3 -> 1 # 13/3 = 4 remainder 1

13 % 4 -> 1 # 13/4 = 3 remainder 1

13 % 5 -> 3 # 13/5 = 2 remainder 3

13 % 6 -> 1 # 13/6 = 2 remainder 1

13 % 7 -> 6 # 13/7 = 1 remainder 6

13 % 8 -> 5 # 13/8 = 1 remainder 5

13 % 9 -> 4 # 13/9 = 1 remainder 4

13 % 10 -> 3 # 13/10 = 1 remainder 3

13 % 11 -> 1 # 13/11 = 1 remainder 2

13 % 12 -> 1 # 13/12 = 1 remainder 1

13 % 13 -> 0 # 13/13 = 1 remainder 0

We can conclude that a number qualifies as a prime number when we only get 0 as the result of the modulus when we divide the number by itself. In code, we can implement this as follows:

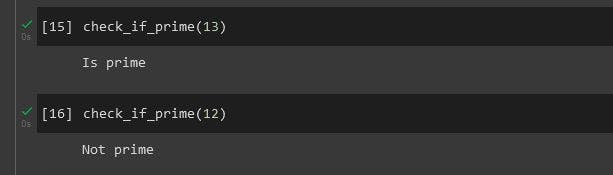
def check_if_prime(x):
      for i in range(2, x):
          if x % i == 0:
             return print("not prime")              
          return print("Is prime")

The code works as expected for checking if a number is prime. We need to modify the code to return a list of prime numbers within a given range. For example, prime numbers between 1 and 100 are:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

Find prime numbers within a range

Working with lists requires the use of nested for loops.

via GIPHY

The complete code is as shown below:

import time    

def check_if_prime(upper_range):

  if upper_range  < 2 :
     return []  
  # append all prime numbers
  list_of_primes = [2] 
  # outter loop from 2 to x
  for number in range(3, upper_range + 1):
      is_prime = True
      # check if the current value of j is prime
      for num in range(3, number):
          # check if j is prime by getting the modulus from 2 to j
          if number % num == 0:
             # if num is not prime break loop and moves to the next value in the range and change is_prime to false
             is_prime = False
             break
      # if  the number is prime, append it to the list
      if is_prime :
        list_of_primes.append(number)             
  return  list_of_primes         

tic = time.perf_counter() # start time
primes = check_if_prime(100000)
toc = time.perf_counter() # End Time

print(primes)
# TIME TAKEN
print(f"Build finished in {toc - tic:0.4f} seconds")

Going over the code above:

• The function takes in a number as a parameter. The parameter represents the maximum value in a range. For example, if we need to find the prime numbers between 0 and 1000, 1000 would be the upper_range

• Initialize a list that will hold all the prime numbers of the given range. The list initializes at 2 since 2 is the first prime number. Any number below two returns an empty list.

• Create an outer for loop that loops through 0 to the upper_range. We add one since the range function excludes the upper range.

For example, when finding the range from 0-5, the range function only works from 0-4. Therefore, if we need the 5 included, we need to add 1 -i.e., from 0-6.

• Initialize a boolean that tracks if the current digit is a prime. It initializes as True and changes to False when the modulus yields a zero.
• The inner for loop checks the specific if the digit is a prime number. This is the same implementation we had earlier on for a single number.
• In the event, the number is prime, the is_prime variable changes to False and is appended to the list_of_primes list.
• lastly, we measure how long this algorithm takes when the upper_range supplied is 100000. It takes 47.34 seconds.

Optimization

We can tweak the algorithm to be more efficient.

• All even numbers are not prime numbers since they are divisible by 2. Thus if a number is not divisible by 2, what's the point of dividing by 4,6, or 8? Essentially, we can eliminate even numbers.

• Consider the number 80. Below are all the factors of 80

    2 *  40 = 80
    4 *  20 = 80
    5 *  16 = 80
    8 * 10 = 80
  10 * 8 = 80 # from here, we are repeating the factors in a different order
  16 *  5 = 80
  20 *  4= 80
  40 *  2= 80

• Once we get to 8 *10, the factors don't change—the order changes with the bigger number starting. Coincidentally, the square root of 80 is 8.94427191. We can then reduce iteration up to the square root of the number when looking for primes.

• Lastly, we use the existing prime values to get the modulus in the inner loop.

def check_if_prime(upper_range):

    if upper_range  < 2 :
       return []

    list_of_primes=[2] 

    for number in range(3, upper_range+1, 2):
          is_prime = True
          square_root_stop = number**0.5
          for num in list_of_primes: # <---only use primes
                if num > square_root_stop: # <--- square root
                      break
                if number % num == 0:
                      is_prime = False
                      break
          if is_prime:
                list_of_primes.append(number)
    print(list_of_primes)
    return list_of_primes     

tic = time.perf_counter() # 
primes = check_if_prime(100000)
toc = time.perf_counter() # End Time
# Print the Difference Minutes and Seconds
print(f"Build finished in {(toc - tic)/60:0.0f} minutes {(toc - tic)%60:0.0f} seconds")
# For additional Precision
print(f"Build finished in {toc - tic:0.4f} seconds")

This reduces the runtime of our algorithm by 46 seconds! Amazing!

via GIPHY